Standard Deviation: Everything You Need to Know for Surveys

Imagine you run a customer satisfaction survey for a popular café chain. You expect most customers to rate the coffee highly—after all, your café prides itself on quality control and excellent service. But when you look at the results, the ratings are all over the place. Some customers give you glowing reviews, while others seem to have had a poor experience. What’s going on? This is where standard deviation helps with quantifying your data, allowing you to understand whether the responses you receive are closely aligned or if they vary wildly. With this method, you can uncover whether those few low scores are outliers, or if your brand’s offerings are truly inconsistent What is Standard Deviation? At its core, standard deviation measures how spread out the values in a dataset are. It tells you how much individual responses deviate from the average, helping you understand whether your data is consistent or has significant variability. In survey analysis, standard deviation gives you deeper insights into how people respond, making it a valuable tool for interpreting results. For example, if all your customers rate your service an 8 or 9 out of 10, you’d have a small standard deviation, meaning the results are fairly consistent. On the other hand, if some rate it a 2 and others a 10, the standard deviation will be much larger, signaling more diverse opinions. The symbol for standard deviation is “σ” (lowercase sigma) for population standard deviation, and “sss” for sample standard deviation. It’s a shorthand used in statistical equations and formulas to denote variability. The Importance of Standard Deviation in Surveys Standard deviation provides a measure of reliability in responses. While the mean (or average) score might give you a quick summary, standard deviation adds context. It shows whether most responses are clustered around that average or if they’re spread across a wide range. A small standard deviation suggests consistency, while a large one points to variability—which may indicate differences in interpretation or experience. This measurement allows researchers and businesses to see beyond the surface of survey data, helping them to identify areas where opinions diverge, and ultimately guiding more targeted improvements or changes. Calculating Standard Deviation Step-by-Step, with an Example Calculating standard deviation might seem complex at first, but it’s a step-by-step process that becomes easier with practice. First, calculate the mean (average) of your data set. Then, subtract the mean from each data point, square the result, and find the average of these squared differences. Finally, take the square root of this average to get the standard deviation. 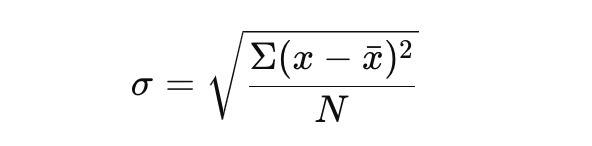Let’s begin by using the following formula: This formula gives you a clear picture of the variability in your data set. Let’s say you conducted a survey asking 5 customers to rate their satisfaction with your service on a scale of 1 to 10. The responses were: 7, 8, 6, 9, 10. Now, let’s calculate the standard deviation for this dataset: Step 1: Find the Mean (Average) To find the mean, add all the data points together and divide by the number of responses. 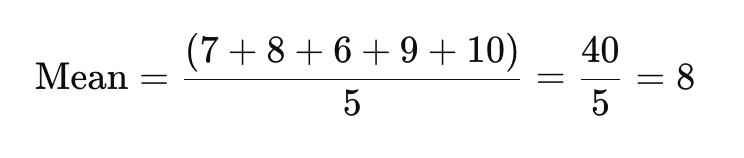The mean satisfaction score here is 8. Step 2: Subtract the Mean from Each Data Point and Square the Result Next, for each score, subtract the mean (8), then square the result. This removes negative values and highlights deviations. 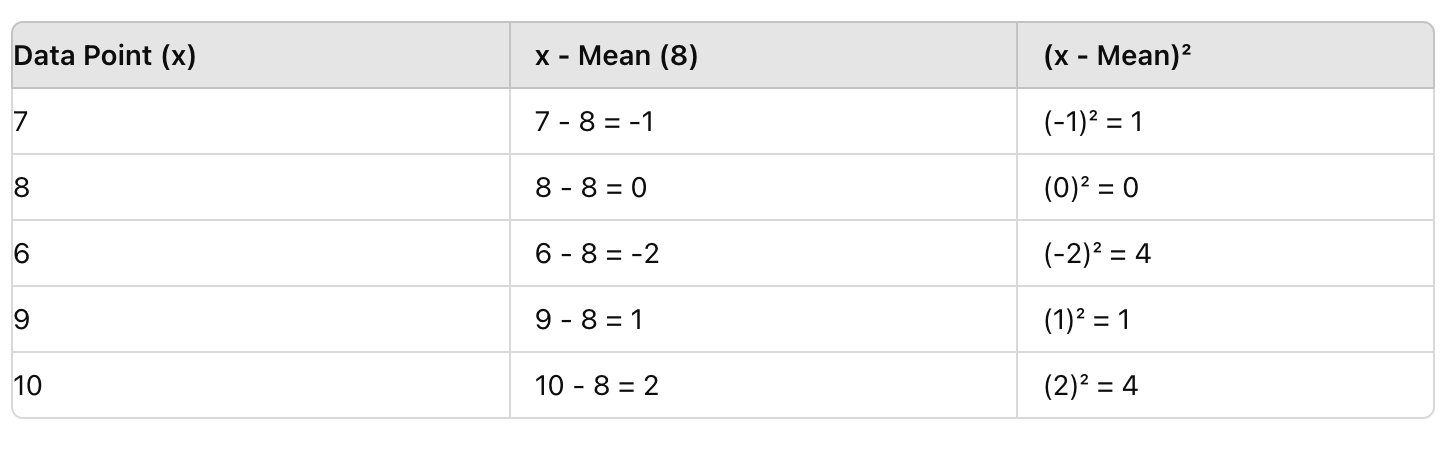Step 3: Find the Mean of the Squared Differences Now, add up the squared differences and divide by the number of data points to find the variance. 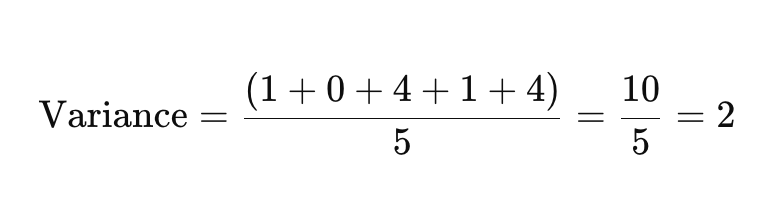Step 4: Take the Square Root of the Variance Finally, take the square root of the variance to find the standard deviation. In this example, the standard deviation is approximately 1.41. This means that most of the customer satisfaction scores are within 1.41 points of the mean score (8). Since the standard deviation is relatively small, the ratings are fairly close to the average, indicating consistency in the feedback. If the standard deviation were larger, say 3 or 4, it would suggest a wider spread of responses, with some customers much more or less satisfied than others. Standard Deviation in Excel Step-by-Step Guide to Using Excel for Standard Deviation Microsoft Excel or Google Sheets is one of the most convenient tools for calculating standard deviation. Here’s how to do it: Enter your data into a column. Select an empty cell where you want the result. Use the formula =STDEV.P() for population standard deviation or =STDEV.S() for sample standard deviation. Highlight your data, press Enter, and Excel will instantly calculate the result. Excel automates the process, saving you time and reducing the potential for manual errors. Exporting LimeSurvey Data to Excel With LimeSurvey, you can export your survey data directly to Excel to further analyze your results. To do this: Navigate to the results section in LimeSurvey. Select the export option and choose Excel as the format. Once exported, use Excel’s statistical functions, including standard deviation, to get a deeper understanding of your data. By combining LimeSurvey’s data collection capabilities with Excel’s analysis tools, you can efficiently interpret and act on your survey results. Understanding Standard Deviation Standard Deviation vs. Standard Error Standard deviation and standard error are related, but serve different purposes. Standard deviation measures the spread of individual data points, while standard error measures the accuracy of the sample mean compared to the true population mean. In surveys, standard deviation helps you understand the variability in responses, while standard error is useful for estimating how close your sample mean is to the actual population mean. Standard Deviation vs. Variance Variance is another measure of data dispersion, and is the square of the standard deviation. While variance helps quantify the magnitude of variability, standard deviation is easier to interpret because it’s expressed in the same units as your original data. For example, if you’re measuring satisfaction scores, standard deviation will provide an intuitive understanding of how much responses differ from the average. Interpreting Standard Deviation Results Once you’ve calculated the standard deviation, you can use it to interpret the consistency of your survey responses. A low standard deviation means that respondents are generally in agreement, while a high standard deviation signals varying opinions. For example, imagine you surveyed 100 employees about their job satisfaction on a scale of 1 to 10. If most responses are clustered around 8, with a small standard deviation, it suggests general satisfaction. However, if the ratings range from 4 to 10, the larger standard deviation shows that opinions are more divided, and you may need to investigate further. Practical Applications of Standard Deviation Improving Survey Questions: If you notice a large standard deviation for a specific survey question, it might indicate that the question is ambiguous or not well understood by respondents. Refining the wording can help gather more accurate data in future surveys. Making Data-Driven Decisions: Standard deviation helps you make more informed decisions by revealing patterns in your survey data. For instance, if feedback is highly variable, you can segment your audience and tailor responses accordingly. Ensuring Accuracy in Standard Deviation Missing Data: Missing data can distort your standard deviation calculation. To avoid inaccuracies, either account for missing data by excluding incomplete responses or use imputation techniques. Avoiding Outliers: Double-checking your data for errors or outliers is essential. Even one incorrect entry can significantly alter your results. Using LimeSurvey’s survey tools can help you collect accurate, usable data that reflects true variability. By starting with an understanding of standard deviation, you’ll unlock powerful insights into your survey results. This allows you to not only interpret the data more effectively, but also make better decisions based on a deeper understanding of how your respondents feel, act, or think. After determining the standard deviation, LimeSurvey allows you to improve your questions, so you can make the most of your survey and data. Give it a try today!