Table Content
You’ve just wrapped up a survey and the results are in—80% of respondents are raving about your new product. Though you want to start celebrating immediately it’s important to remember the little ± number also known as the margin of error at the bottom of your survey results—because it might just serve as a reality check.
In the world of survey research understanding the margin of error isn’t just a nice to have; it’s essential. Without it even the most promising results can be misleading. The margin of error provides context helping you make informed decisions based on the data collected.
What is the Margin of Error?
The margin of error is a statistic that quantifies the uncertainty in your survey results. It represents the range where the true population parameter is expected to fall providing a certain confidence level and accounting for the fact that you’re surveying a sample of the population rather than the entire population.
A smaller margin of error indicates that your survey results are more likely to be close to the true population values while a larger margin of error suggests greater uncertainty and a wider range of possible outcomes. The acceptable margin of error falls between 4% and 8% at the 95% confidence level.
Understanding Margin of Error in Research
In survey research the margin of error is essential for interpreting the reliability of your results. When you collect data using LimeSurvey you’re often working with a sample of the population. The margin of error helps you understand how close your sample results are to what you would expect if you surveyed the entire population.
Explanation and Usage of the Margin of Error Symbol
The margin of error is typically represented by the symbol ± and followed by a percentage. Let’s say your LimeSurvey results show that 60% of respondents prefer a certain product with a margin of error of ±4%. This means the true population value is likely between 56% and 64%.
This symbol is a shorthand way of expressing the range where the true population parameter lies. It is widely used in research polling and any scenario where data is gathered from a sample.
Calculate Margin of Error in 3 Steps
1. Determine the Z-score: The Z-score corresponds to the desired confidence level representing how far a data point is from the mean in standard deviation units. For reference, a 95% confidence level is associated with a Z-score of 1.96, while a 99% confidence level corresponds to a Z-score of 2.58.
| Desired confidence level | Z-score |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. Identify the standard deviation or proportion: The standard deviation measures the amount of variation in your data. If you’re dealing with proportions (e.g., the percentage of respondents who chose a specific option), you’ll use the proportion in place of the standard deviation.
3. Calculate the margin of error using this formula:
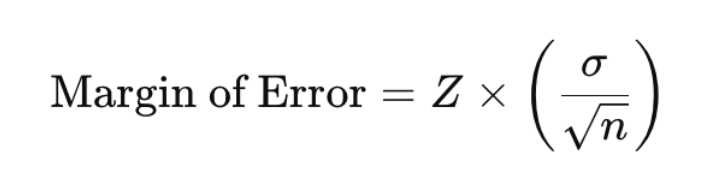
𝜎 represents the standard deviation, 𝑛 is the sample size, and 𝑍 is the Z-score. The formula highlights the inverse relationship between sample size and margin of error: as the sample size increases, the margin of error decreases.
Using a larger sample size will typically yield a smaller margin of error making your findings more reliable. Conversely, a smaller sample size will result in a larger margin of error reflecting greater uncertainty in the data.
For example, if you survey 400 people and find that 50% of them are satisfied with their customer experience with a standard deviation of 0.5 and a 95% confidence level, the margin of error would be calculated as follows:
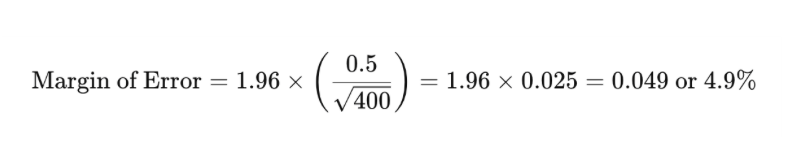
This means that the true percentage of the population that is happy with the customer experience is likely between 45.1% and 54.9%.
Margin of Error Calculator for Your LimeSurvey Project
Several online calculators can help you retrieve the margin of error for your data. To use a margin of error calculator, you need to input your desired confidence level, the sample size, and either the standard deviation or the proportion. The calculator will then output the margin of error.
Differences Between Margin of Error and Standard Error
The margin of error quantifies the uncertainty in your survey results, specifically the range within which the true population parameter is expected to fall based on your sample data. It is often expressed as a percentage and is used to provide a confidence interval around a survey estimate.
On the other hand, the standard error (SE) measures the variability or dispersion of a sample statistic such as the sample mean from the population mean. It gives an indication of how much the sample statistic is expected to fluctuate if different samples were drawn from the same population.
The standard error is more relevant when performing statistical tests or comparing different samples. Margin of error works best when focusing on the reliability of a single survey result, and standard error is the preference when comparing statistics across samples.
Best Practices for Applying Margin of Error
When conducting research using LimeSurvey, follow these best practices for applying the margin of error can improve the accuracy of your study:
- Ensure adequate sample size: To achieve a low margin of error, researchers should survey a sufficiently large sample that accurately represents the population.
- Consider the population size: While the margin of error is mostly independent of the population size, it’s important to account for it when dealing with very small or very large populations.
- Select an acceptable confidence level: Typically, researchers use a 95% confidence level, which corresponds to a Z-score of 1.96. However, you might choose a higher confidence level such as 99% for greater certainty.
- Be transparent: When presenting your research findings, the margin of error helps others understand the potential variability in your results and provides context for interpreting the data.
- Regularly review and adjust: As your research progresses or as more data becomes available, it’s essential to review your margin of error calculations.
A well-calculated margin of error ensures that your survey results are trustworthy, reflective of the broader population, and honest about any uncertainty in your findings—all of which are vital for maintaining credibility and making informed decisions.
Get Started with LimeSurvey
LimeSurvey offers a suite of user-friendly and comprehensive survey tools that empower you to design highly effective surveys with ease. With these tools, you can create well-structured surveys that not only capture the data you need but ensure that your results come with an optimal margin of error.
This means your surveys won’t just gather responses—they’ll provide insights you can trust, reflecting the true sentiments of your target population. Whether you're a seasoned researcher or a university student, LimeSurvey's intuitive interface will guide you every step of the way, making sure your survey data is both accurate and actionable.

